故事的开头

怀着激动的心情，朋友告诉我他在游戏中出了一把极品锻造神器。

因为神器的材料是稀少的，所以我们讨论到在游戏中用其它更平凡的材料进行“垫抽”是否有意义。

摸球假设

为了进一步分析，假设有这样一个摸球游戏：

类型：

• A类是锻造神器
• B类是锻造凡器（用于垫抽）

品质：

• 优等 20\%
• 劣等 80\%

模拟数据

进行 1000 次模拟结果

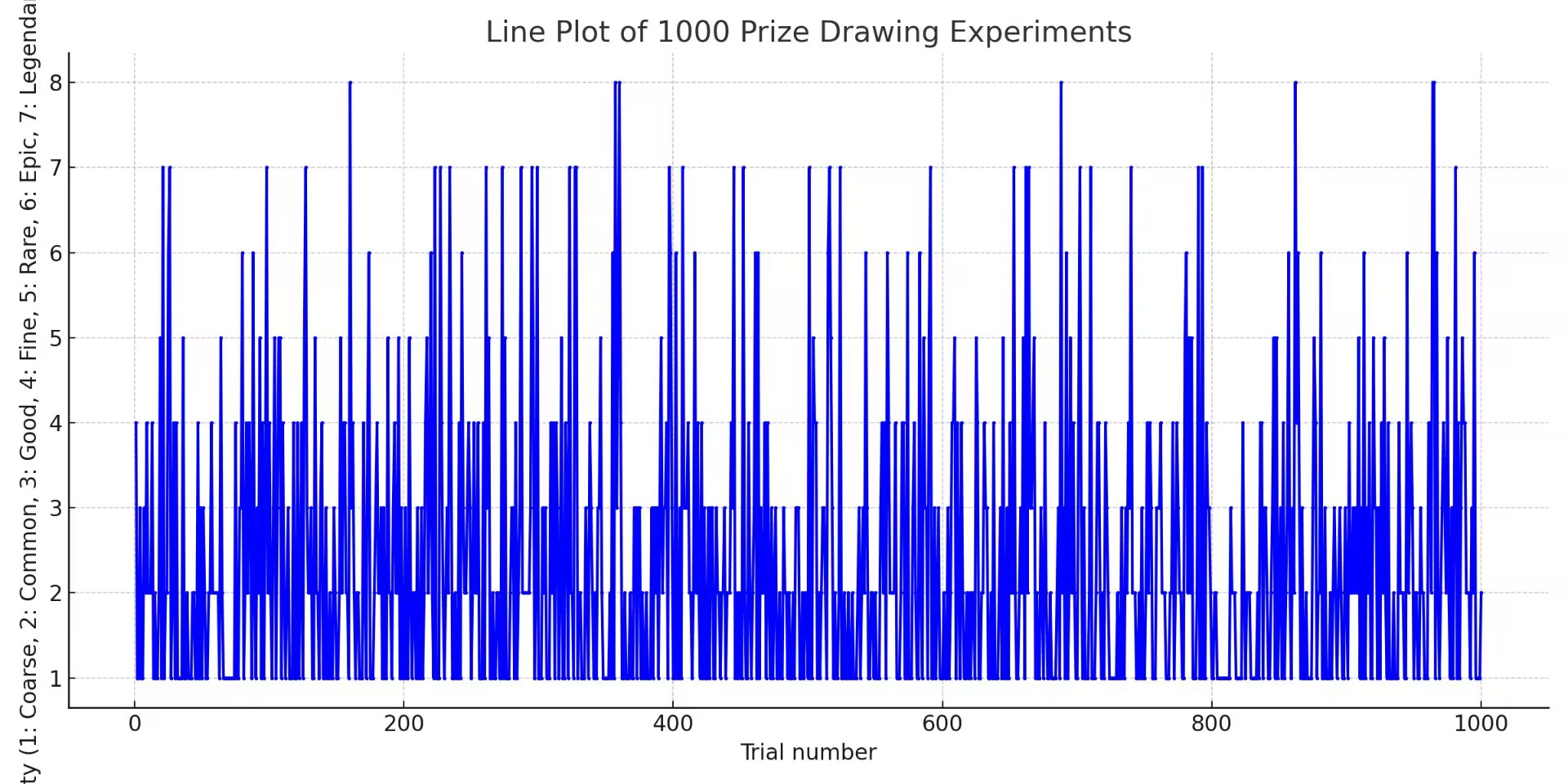
可见相同品质之间存在间距，如 8 级品质，间距约为 200 抽

这是否证明垫抽可以有效提高抽中极品锻造神器的概率呢？

我们先看两个经典问题

蒙提霍尔问题

在一个游戏节目中，参赛者面前有三个门，其中一个门后有一辆汽车（大奖），另外两个门后各有一只山羊（安慰奖）。主持人知道每个门后是什么。当参赛者选择了一个门后，主持人不会立即打开，而是会打开剩下两个门中一个有山羊的门。然后，主持人问参赛者是否要换到另一个未打开的门。

问题

参赛者是否应该换门？换门能否增加赢得汽车的概率？

解答

换门可以增加赢得汽车的概率。初始选择中，参赛者有 \frac{1}{3} 的概率选中汽车，\frac{2}{3} 的概率选中山羊。

主持人打开一个有山羊的门后，若参赛者换门，赢得汽车的概率提升到 \frac{2}{3}。因此，理性选择是换门。

两封信悖论

你面前有两个信封，其中一个信封里的金额是另一个的两倍。你随机选择了一个信封，打开后发现里面有100元。现在你有机会换到另一个信封。

问题

你是否应该更换另一封信封？更换另一封信封能否增加获得高额奖金的概率？

解答

直觉上，你可能认为另一个信封有50%的概率是50元，50%的概率是200元，所以期望值是：

这比手中的100元要高，似乎总是应该换。但按照这个逻辑，无论信封里有多少钱，你都应该换，这就产生了悖论。

这个悖论的关键在于错误地计算了期望值。实际上，信封内金额的分布并非均匀，换信封并不会带来额外的期望收益。正确的分析应考虑初始金额的不确定性，而不是简单地平均可能的结果。